|
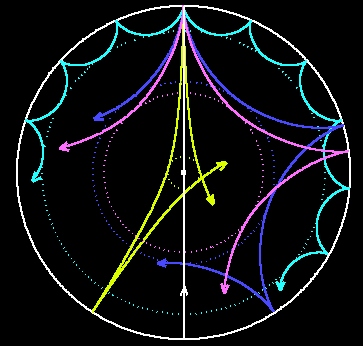
Die Moden auf der Sonne bilden sich aus aufgrund von Resonanz-Wellen im Inneren der Sonne.
|

Die Moden auf der Sonne bilden sich aus aufgrund von Resonanz-Wellen im Inneren der Sonne.
| Betrachtet man das
Sonnensystem vom nördlichen Pol der Ekliptik aus, dann kann man
die Winkelabstände der Planeten untereinander erkennen. Auffällig
ist nun, daß zu bestimmten Zeiten, wenn die Planeten harmonische
heliozentrische oder geozentrische Positionen auf der Ekliptik einnehmen,
auf der Sonne, resp. auf der Erde dramatische Ereignisse geschehen.
Auf der Sonne kommt es in Verbindung mit der Harmonie des Sonnenfleckenzyklus zu sogenannten Flares, Ausbrüchen von Sonnenmasse, welche Teilchen dann fast mit Lichtgeschwindigkeit von der Sonne hinaus in den Weltraum beschleunigen. 
credits and thanks to NASA/SOHO Diese Animation ist die Darstellung eines Ausbruchs auf der Sonne vom 7. April 1997,14:00 UT Flare, 14:01 - 14:50 Shock, 15:00 - CME (Massenausstoß). Zu dieser Zeit hatten die Planeten folgende heliozentrischen Winkelbeziehungen untereinander:
* Am 23. Februar 1956, zu Anfang des Sonnenfleckenzyklus, der mit einer Sonnenfleckenzahl von über 250 im Oktober 1957 sein Maximum erreichte, erfolgte der größte jemals gemessene Ausbruch (Klasse 4 ) dieser Art auf der Sonne um 3 Uhr 33 UT. Zu diesem Zeitpunkt gab es einige besonders auffällige heliozentrische Planetenaspekte. Jupiter und Pluto hatten die gleiche Position auf der Ekliptik, sie standen nur etwa 0.33° auseinander (Konjunktion). Dazu stand Saturn 90° (Quadrat) mit einer Abweichung von etwa 0.2-0.5° zu Jupiter/Pluto. Und letztlich standen Merkur und Mars zusammen (Konjunktion) mit einem Abstand von etwa 0.07°. Uranus und Neptun bideten einen Winkel von 88,02°. Sie bilden aber auch mit ihren Abständen zu Pluto, Jupiter und Saturn mit Winkel von etwa 30° harmonische Aspekte. Diese Verhältnisse sind in der folgenden Grafik wiedergegeben, in dem die Planetenabstände von der Sonne logarithmisch dargestellt sind (in A.U.), und in der auch die Lage ekliptikalen Sonnenäquators eingezeichnet . 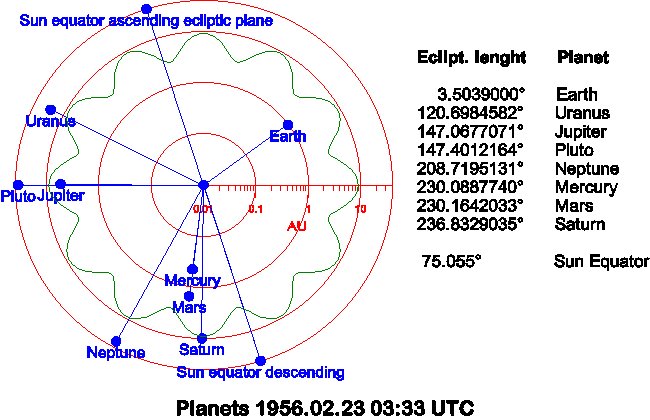 Die Sonne dreht sich um eine Achse, welche um 7.25° gegenüber der Ekliptik gekippt ist, und wie es scheint und Jack Eddy herausfand, treten die regelmässigen Sonnenflecken, die sonst alle 11 Jahre auftreten, dann nicht auf, wenn einige Planeten einen harmonischen Aspekt zu der Richtung des Sonnenäquators bilden, wie z.B. in den Jahren von 1645 bis 1715, in dem sogenannten Maunder Minimun. Ähnlich der
Moden auf der Sonne könnten auch auf der Erde solche Schwingungsmoden
mit bestimmten Modenzahlen von z.B. 2, 3, 4, 6, 8, 12 auftreten,
wenn die Erde dazu angeregt wird.
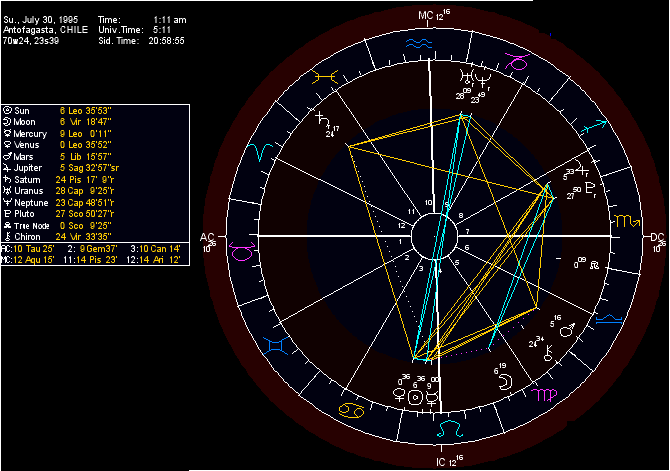
grafic: astrodienst ch |
*
| Das Erdbeben von Kobe, Japan am
16. Januar 1995 um 20 Uhr: 46 min 52.1 sec UTC N34.583, E135.018.
Zu erkennen sind die Moden
8 und 4, hervorgehoben durch blaue
Linien. Die Moden 6 oder 3 sind nicht (!) beteiligt. In der folgenden Tabelle
sind die genauen Daten aller beteiligten Moden aufgeführt. Gelistet
sind Planet, der Winkel zur Himmelsmitte (M.C.) bezogen auf den Ortsmeridian
von Kobe, die ekliptische Länge des Planeten (oder M.C.), die Modenzahl
als ganzer Wert durch den der ganze Kreis von 360° geteilt und bezogen
ist auf den M.C., der Moden Winkel und der Fehler in ° den ein Planet
jeweils zum exakten Modenwinkel hat. Der M.C. lag zur Zeit des Bebens
auf 24° 33' Waage entsprechend einer ekliptischen
Länge von 204.55°.
Die Moden 8 und 10 des Kobe Bebens sind hier noch einmal, wie sie symmetrisch zum M.C. auftreten, dargestellt. Dabei zeigen Merkur und Pluto jeweils ein Maximum der Mode 10 (Grün) und Sonne, Mond, Venus, Jupiter, Saturn, Uranus, Neptun ein Maximum der Mode 8 (Blau). Der M.C. liegt auf dem Winkel = 0° der Ekliptik. |
|
|
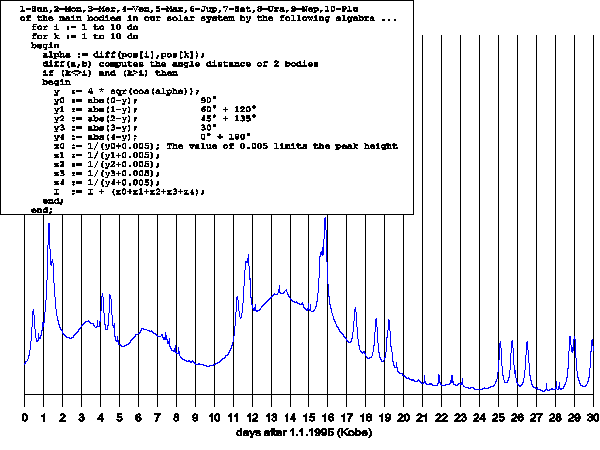
Mit einem sehr einfachen Kreis-Algorithmus kann man den Grad der harmonischen Verteilung aller Planeten auf ganzzahlige Teilungen eines Kreises von 360° (0° 30° 45° 60° 90° 120° 135° 150° 180°) bestimmen:
|
|
 |
|
|
|
|
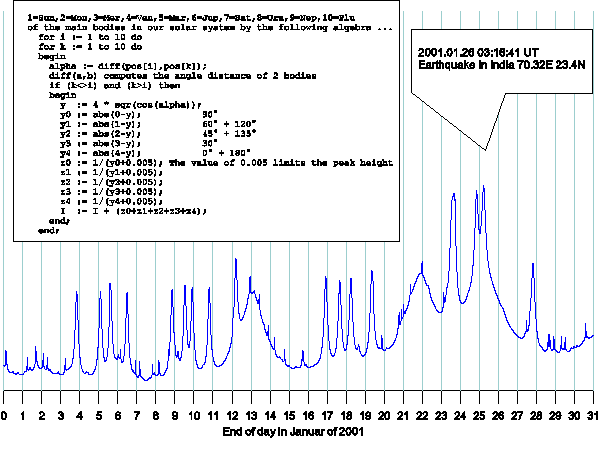 Die statistische
Chance, dass es sich hier um einen Zufall handelt ist geringer als 0.0000001
(!).
Berechnet man den Harmonie Index (s.o) für dem Monat Mai 2008, so zeigt er am
12. Mai zwei große peaks, allein an diesem Tage (UT) ereigneten
sich dort 21 Nachbeben stärker als
MAG 5.0.
Man kann auch zeigen, dass der berechenbare Harmonie Index auch eine Beziehung zu der Anzahl aller weltweit registrierten Beben (magenta) pro Tag (schwarze Rhomben) hat. So ereigneten sich am 12. Mai 2008 weltweit 204 Beben (204/25=8.16) registrierte Beben und am 17. Mai 2008 24 registrierte Beben (24/25= 0.96) weltweit. Geozentrische
ekliptische Längen am 12. Mai 2008 um
06:28:01 UTC = jd (ET)
= 2454598.770323 I II
Winkel
Mode Fehler Ich habe diese Beobachtungen in den newsgroups: sci.geo.earthquakes und de.sci.astronomie veröffentlicht. Aber weder Geophysiker noch Astronomen zeigten ein Interesse für diese Beobachtungen. Thanks to Astrodienst CH |
|
s.a. Brian Johnston: "Planetrary
Aspects And Terrestrial Earthquakes" http://cura.free.fr/xv/13brianj.html

volker doormann |